En promedio, ¿de cuántas formas se puede expresar un número como suma de dos cuadrados perfectos?

Hace un mes, leí la siguiente cita en el blog Futility Closet:

Every now and again one comes across an astounding result that closely relates two foreign objects which seem to have nothing in common. Who would suspect, for example, that on the average, the number of ways of expressing a positive integer n as a sum of two integral squares, x²+y²=n , is π?

De vez en cuando uno se encuentra con resultados sorprendentes que relacionan estrechamente dos objetos extraños que no parecen tener nada en común. ¿Quién podría sospechar, por ejemplo, que en promedio, el número de formas de expresar un entero positivo n como suma de dos cuadrados enteros, x²+y²=n, es π?

Ross Honsberger

Esta cita me cautivó, sobre todo, por el ejemplo que proponía. Parecía tan sencillo... así que me puse a buscar referencias. Prácticamente en todos los sitios que miraba, lo daban como un hecho elemental que, probablemente, se deba a Ramanujan, pero en ningún lugar encontraba una prueba. Así que me fui a preguntar un compañero experto en Teoría de Números para que me diera alguna referencia. Sin embargo me dio algo mucho mejor. Me propuso enseñarme una prueba in situ en su pizarra... y acepté. Tanto la explicación como la propia prueba me fascinó por su simplicidad y su belleza. Así que he decidido mostrarla a todos mis lectores para que todos os podáis deleitar con ella. Allá vamos.

Antes de empezar vamos a centrar un poco las ideas. En el fondo, nos estamos preguntando por las formas que hay de expresar un número natural como la suma de dos cuadrados de números enteros. Por ejemplo, , , pero no hay forma de expresar el 7 como suma de 2 cuadrados. Además, si nos ponemos quisquillosos y tomamos en cuenta signos y orden, podríamos decir que

¿Y por qué vamos a hacer esto? Pues porque en realidad estamos buscando soluciones enteras de la ecuación para y todos los pares anteriores son soluciones diferentes de la ecuación para .

Pues vamos a ponerle nombres a las cosas. Vamos a llamar al número de formas de expresar el número como suma de 2 cuadrados de números enteros; y en esta forma vamos a tener en cuenta lo anterior, es decir, que nos importará el orden y el signo. Visto así,  podemos afirmar que , que , que o que (si quieres, puedes ver los primeros valores de en la sucesión Sloane's A004018).

Con esta notación, lo que la cita afirma es lo siguiente:

¿Que no lo ves? pues vamos poquito a poco. Como hay infinitos números naturales, si queremos hacer la media de todos los valores, tendríamos que hacer una suma infinita (serie) y dividir entre el número de sumandos (infinitos)... lo que, en mi modesta opinión, puede acarrear algunos problemillas. No, así no podemos hacerlo. Así que mejor tomar los primeros valores de (desde hasta ), los sumamos y dividimos entre el número de sumandos: . Ahora, basta con hacer que el número de sumandos sea cada vez mayor y mayor, o como decimos los matemáticos, hacemos que .

Pues vamos a calcular ese límite. Lo primero que podríamos pensar es conseguir una fórmula exacta para calcular . A este respecto, existen varios resultados: por ejemplo, Fermat demostró que si es un número primo, entonces es expresable como suma de cuadrados si y sólo si ó , lo que nos lleva a que si en otro caso, se tendría que (como ocurre para o ). Existe una formulación exacta para calcular , pero escribirla es demasiado complicada. Si quieres, puedes encontrarla en [1, Theorem 4.4].

Así que el método "a lo bestia" de calcular todos los valores implicados y sumar, se nos va al traste. Vámonos a dar un paseo por la geometría a ver si nos ayuda.

Tomemos el plano real y tracemos el mallado entero, es decir, todas las rectas de la forma e con . Los puntos de corte de dicha malla son, precisamente todos los puntos con ambas coordenadas enteras. Pero mejor mirad el dibujo:

Sobre esta malla, vamos a dibujar la circunferencia centrada en el origen y de radio

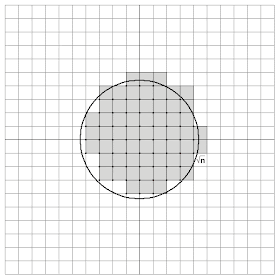
 Ahora nos fijamos en los puntos del mallado que caen DENTRO de esta circunferencia:

Los puntos marcados son todos los puntos con ambas coordenadas enteras y tales que ; pero como resulta que por lo que el número de puntos dentro del círculo de radio coincide precisamente con , es decir, todas las formas que hay de escribir los números menores (estrictos) que , como suma de dos cuadrados de enteros.

Pero claro, si ahora queremos estimar o calcular el número de puntos dentro de un círculo, nos enfrentamos a un problema bastante complicado. Así que vamos a hacer lo siguiente. Cada punto del mallado está en 4 cuadrados (arriba izquierda, arriba derecha, abajo izquierda y abajo derecha), así que a cada punto le haremos corresponder el cuadrado que está arriba y a la derecha de dicho punto.

Bien, ahora hay que darse cuenta de que el área de cada uno de dichos cuadrados es, exactamente 1, por lo que para contar los puntos de la malla que hay dentro del círculo, basta con calcular el área de todos los cuadrados. Sería muy interesante que el área de los cuadrados coincidiese con la del círculo... pero lamentablemente no tiene por qué ser así (hay cuadrados que se salen del círculo y partes del círculo que no están cubiertos por cuadrados). Sin embargo, sí que vamos a poder acotar el área de los cuadrados. Veamos cómo.

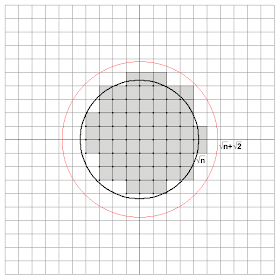
Por un lado, ¿cuánto puede salirse un cuadrado del círculo? En el peor de los casos sería , es decir, la diagonal de un cuadradito:

por lo que podemos asegurar que todos los cuadrados quedarán dentro de la circunferencia de centro el origen y radio

Ahora bien, un punto que esté fuera de la circunferencia original (la de radio ) pero casi casi pegado a ella, dejará casi todo su cuadrado superior derecho dentro de la circunferencia y no será parte de los cuadrados sombreados. En el peor de los casos, la distancia que dicho cuadrado se puede meter dentro de nuestra circunferencia original vuelve a ser ,

por lo que podemos asegurar que la circunferencia de centro el origen y radio caerá siempre dentro del área encerrada por los cuadrados sombreados.

 Así que podemos garantizar que la zona sombreada contiene al círculo azul y está contenido en el círculo rojo. Pero resulta que el área de la zona sombreada era y que las áreas de esos círculos las sabemos calcular, por lo tanto tenemos las siguientes desigualdades:

 

de donde se deduce que

por lo que, dividiendo entre en todos los miembros se concluye que

Ahora basta aplicar la famosa Regla del Sandwich para concluir que

y que, precisamente, nos dice que, en promedio, el número de formas de escribir un número natural como suma de cuadrados (teniendo en cuenta orden de sumandos y signos) es, justamente, .

Para vosotros os dejo que penséis qué ocurre si queremos olvidarnos de signos (en cuyo caso bastaría con quedarnos con la construcción anterior pero únicamente en el primer cuadrante) o qué pasaría si, además, queremos olvidarnos del orden (en cuyo caso... la cosa se pone muy interesante). A este respecto, deciros que, por cada par de naturales con tale que hay 4 variaciones para incluir signos (siempre que ninguno de ellos sea, precisamente 0) y otras 4 de orden (siempre y cuando no sean los 2 iguales... pero ahora que lo pienso... ¿ESO ES IMPOSIBLE!). Así que por cada pareja de números, hay o bien 4 o bien 8 variaciones triviales... y por ahí podéis empezar a pensar.

Tito Eliatron Dixit

Referencias:
[1] Bhaskar, J. "Sum of two squares", disponible en http://www.math.uchicago.edu/~may/VIGRE/VIGRE2008/REUPapers/Bhaskar.pdf

[2] Weisstein, E.W. "Sum of Squares Function." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/SumofSquaresFunction.html

PD: Esta entrada participa en la Edición 4.123  del Carnaval de Matemáticas, cuyo anfitrión es el blog Eulerianos.