Tito Eliatron Dixit: La importancia del -1 y el Último Teorema de Fermat

miércoles, 25 de mayo de 2011

La importancia del -1 y el Último Teorema de Fermat

¿Cuántas veces nos han dicho los alumnos eso de "jo, por un signo"? Una de las respuestas más típicas es la de "eso, si al arquitecto le sale el puente del revés, dirá que es por un signo"; o bien aquélla que arguye temas más pecuniarios "claro, es lo mismo tener 1000€ que deber 1000€".

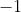
En cualquier caso, todo depende de un signo, o visto de otro modo, de un $-1$ . A continuación vamos a comprobar ómo puede afectar a uno de los teoremas más conocidos de las matemáticas, el Último Teorema de Fermat. Hace ya algún tiempo, vimos por aquí una variante a la que llamamos Teorema de Tamref, ahora os propongo la siguiente:

Demostrar que la ecuación 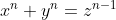$x^n+y^n=z^{n-1}$ tiene solución entera ( 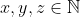$x,y,z\in\mathbb{N}$ ) para cualquier 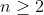$n\ge 2$ entero.

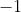
¿Véis la diferencia? en realidad es un simple $-1$ , un signo, vamos. Pues bien, lo curioso del caso es que no es demasiado complicado ver que este problema tiene infinitas soluciones.

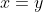
Os voy a dejar una sencillita, pero que sepáis que hay otra. En primer lugar, vamos a intentar resolver en un caso particular, aquél en que $x=y$ . Entonces nuestra ecuación queda de la forma

$2x^n=z^{n-1}$
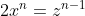
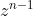
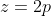
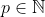
¿Qué hace falta entonces para que se dé esta igualdad? pues lo primero es que $z^{n-1}$ debe ser par, lo que implica que (por aquello de par por par, par; impar por impar, impar) $z$ debe ser par, es decir, $z=2p$ con $p\in\mathbb{N}$ . Por lo tanto, la nueva ecuación será

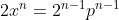$2x^n=2^{n-1}p^{n-1}$ o lo que es lo mismo $x^n=2^{n-2}p^{n-1}$ .
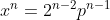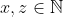
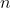
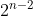
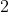
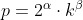
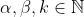
Para que esta ecuación tenga solución entera, es decir, que $x,z\in\mathbb{N}$ , el segundo miembro tendría que ser una potencia enésima, es decir, algo elevado a $n$ . Para ello, como ya tengo un factor $2^{n-2}$ , $p$ debería aportar algún otro factor $2$ para que compense. Me explico mejor. Vamos a buscar $p$ de la forma $p=2^{\alpha}\cdot k^{\beta}$ con $\alpha,\beta,k\in\mathbb{N}$ a elegir.

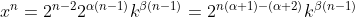
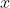
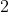
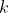
Si ponemos todo junto, resulta que $x^n=2^{n-2}2^{\alpha(n-1)}k^{\beta(n-1)}=2^{n(\alpha+1)-(\alpha+2)}k^{\beta(n-1)}$ . Ahora bien, para poder extraer "raíz enésima" en ambos miembros de la ecuación (y poder despejar la $x$ ), debe ocurrir que el exponente del $2$ y el de $k$ sean múltiplos de $n$ .

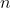
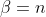
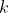
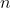
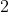
Por lo pronto, podemos elegir $\beta=n$ y así el exponente de $k$ será múltiplo de $n$ . Para arreglar el exponente del $2$ , podemos elegir $\alpha+2=n$ .

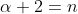
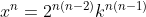
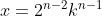
De esta forma, nos queda $x^n=2^{n(n-2)}k^{n(n-1)}$ , de donde $x=2^{n-2}k^{n-1}$ . Y por otro lado, $z=2p=2\cdot 2^{n-2}k^n=2^{n-1}k^n$ .

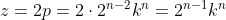
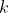
¿Y cómo elegimos $k$ ? Pues esto es lo mejor de todo: como queramos. Con lo que nuestro problema, no sólo tiene solución, sino que, además, hay infinitas soluciones.

Es evidente que este método no sirve para el verdadero Último Teorema de Fermat, y esto os lo dejo a vosotros. También os dije que hay más soluciones, pero también os dejo a vosotros cómo obtenerlas:

$x=k(k^n + 1)^{n-2}$ , $y=(k^n + 1)^{n-2}$ , $z=(k^n + 1)^{n-1}$ .

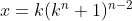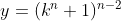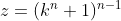Tito Eliatron Dixit

PD: Esta entrada forma parte de la Edición 2.4 del Carnaval de Matemáticas cuyo anfitrión es el blog Seis Palabras.

Referencias:
Minus one, but what difference de Kut the Knot
What a difference a minus one makes! de CTK Insight

1 comentario:

Curso Community Manager1 de junio de 2011, 9:39
Nunca he sido experto en Matemáticas, creo que mi cabeza es demasiado complicada como para poder resolver estos enigmas. No había oído hablar del Teorema de Fermat hasta que leí Millenium 2, donde la protagonista se desvive por resolverlo.

Me encantaría tener esa capacidad, pero que le vamos a hacer.
ResponderEliminar
Respuestas