Se trata de demostrar que la ecuación
no tiene soluciones enteras para 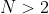 , porque, claro, si
, porque, claro, si 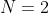 es evidente que sí hay soluciones. Por ejemplo, basta tomar
es evidente que sí hay soluciones. Por ejemplo, basta tomar 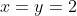 y
y 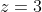 ; o bien
; o bien 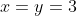 y
y 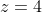 .
.
No, no me estoy volviendo loco. Esto no es el Último Teorema de Fermat. Pero digamos que la relación que tiene con él es la misma que la Conjetura de Hcabdlog con la archiconocida Conjetura de Goldbach.
Si en una semana no han dado con la solución, os la dejaré en un artículo. En la fuente original [1] viene cómo resolverlo, así que lo suyo sería no mirarla.
Aunque, ahora que lo pienso, os dejo con un problema derivado que se me acaba de ocurrir y cuya solución no viene en la fuente.
Para
¡Hala! Ahí queda eso.
Tito Eliatron Dixit
REFERENCIA:
[1] Su, Francis E., et al. tamreF's Last Theorem, Math Fun Facts.

Creo que sé hacerlo, y bastante fácil que sale, pero como es el primer comentario de la entrada, mejor no digo nada para que la gente lo piense. Doy un par de pistas (que sois libres de leer o no).
ResponderEliminar1-Si no os gustan los valores enteros, intentad resolverlo con naturales ya que al fin y al cabo es fácil pasar de un caso al otro (multiplicando por N^a con a suficientemente grande).
2-Para el caso N=2, hay infinitas soluciones. Concretamente hay una solución y solo una solución para cada valor entero que puede tomar x.
Espero no haber metido la pata en ninguno de los 2 comentarios anteriores ya que ni me he parado a escribir nada.
@Carlos: muy buenos e interesantes los apuntes que das. De la unicidad no estaba seguro... pero me he convencido de que es cierta. Cosa que también habría que probar, claro. jejeje
ResponderEliminarDivídase por N^y y ya sale todo lo que dice Carlos.
ResponderEliminarSi, creo que lo he visto. Un ligero "spoiler" un poco más abajo. Por si no lo quieren leer...
ResponderEliminarPara N=2, la unicidad es lo interesante y está implicita en la demostración principal (con alguna observación adicional), pero hay solución si (y solo si) x=y=z-1
Jejeje, veo que acabas de conocer Math Fun Facts. Gran fuente, sí señor. Yo también hablé hace tiempo del teorema de tamreF y de alguna cosa más de esa página, y tengo idea de publicar algún tema más que he visto allí.
ResponderEliminarMás que descubror, ^DiAmOnD^, diría RE-descubrir.
ResponderEliminarLa página la conocía, pero no había curioseado lo bastante.
Respecto a tu artículo de Tamref... pues no lo había vistyo, la verdad.
Y a ver si nos ponemos de acuerdo en qué ideas tomamos de allí, no vayamos a publicar los 2 lo mismo el mismo día xDDD
Lo de la unicidad de que para valor entero x hay una única solución cuando N=2 es también fácil de ver. Doy pista, el que no la quiera que no siga leyendo...
ResponderEliminarClaramente 2^(maximo{x,y})<=2^x+2^y<= 2^(maximo{x,y}+1)
y de aquí se puede deducir la unicidad.
En mi comentario anterior, el primer <= era un < estricto.
ResponderEliminarPues sí, también es verdad. Yo tengo un par de ideas sacadas de esa página que quiero escribir en las próximas fechas. Si quieres me puedes contar cuáles son las tuyas y te digo yo las mías y así nos podemos coordinar :).
ResponderEliminar