Creo que de todos es conocido el hecho de que
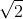
es irracional. Incluso muchos de vosotros seríais capaces de darme una demostración. Los griegos clásicos, coetáneos de Pitágoras, fueron capaces de demostrar que todas las raíces de números naturales entre 2 y 17 (excepto 4, 9 y 16) eran números irracionales. El motivo por el que pararon en 17 no se sabe con certeza, pero parece que la demostración usada (por
Teodoro de Cirene) tenía un carácter geométrico que impedía ir más allá. A lo mejor, la
Espiral de Teodoro puede tener algo que ver.
En el presente post vamos a demostrar que la raíz cuadrada de un número natural que no sea un cuadrado perfecto, debe ser irracional. Y lo vamos a probar usando métodos que hasta el propio Pitágoras podría haber conocido. Vamos allá.
Tomemos un número natural
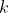
que no sea un cuadrado perfecto. Supongamos,
por reducción al absurdo, que

es racional, es decir,

donde
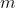
y
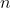
son naturales (con

, por si eres de los que cuenta el cero entre los naturales). Como
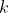
no es un cuadrado perfecto, es claro que
 no
no es natural, por lo que podemos encontrar

de forma que

, luego

.
Como

, elevando al cuadrado y quitando denominadores se consigue que

. Si ahora restamos

en ambos miembros y sacamos factor común llegamos a que

, y de aquí es fácil deducir que

.
Sabemos que

, por lo tanto,

, de donde

.
Por otro lado, como

, se tiene que

. Pero ya sabemos que

, por lo que

o lo que es lo mismo,

.
Si llamamos

y

, lo que acabamos de probar es lo siguiente. Si

con

y

, entonces existen otro par de naturales

tales que

,

y

. Repitiendo este proceso, partiendo de

, encontraremos otro par de naturales

tales que

,

y

.Como podéis imaginar, este proceso lo podemos repetir
ad infinitum... y encontraríamos sucesiones infinitas de naturales estrictamente decrecientes, lo que es una clara
contradicción, pues los números naturales tienen un primer elemento.
Por consiguiente, la hipótesis de partida ha de ser falsa y nunca podremos encontrar números naturales

tales que

, o dicho de otro modo,
 es irracional.
es irracional.
Este método de demostración, en realidad, es una variante de la inducción que se conoce como
descenso infinito y fue desarrollado por
Pierre de Fermat. De hecho es posible que hayas visto antes otra demostración por descenso infinito... la de la
irracionalidad de 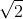 basada en la paridad
basada en la paridad. Y si tienes un poco de paciencia... quizás te enseñe alguna que otra curiosa demostración en este mismo blog.
Fuentes:
Infinite descent en Wikipedia (En).
Y. Sagher, What Pythagoras could have done, Amer. Math. Monthly 95 (1988), 117.
Tito Eliatron Dixit

Sobre la demostración de Teodoro de la irracionalidad hasta raiz de 17, ver
ResponderEliminarhttp://gaussianos.com/dos-demostraciones-de-la-irracionalidad-de-raiz-de-2/#comment-1640
Para una discusión de otras hipótesis (incluida la espiral de Anderhub) se puede ver el siguiente enlace
http://www.encyclopedia.com/doc/1G2-2830904280.html
A pesar de la amplia bibliografía que contiene, no se menciona la propuesta de McCabe esbozada en el primer enlace que, para mi gusto, es la hipótesis más verosímil.
Saludos.
Muchas gracias fede por tan interesante apunte. El post de Gaussianos lo leí para redactar éste, pero ya no los comentarios (grave error).
EliminarQué bonita demostración.
ResponderEliminarSaludos!