El efecto mariposa: una condición superflua del caos

Hace un par de días, publiqué en Amazings la entrada titulada El Efecto Mariposa: vaya ¿timo? que os animo a que leáis. En ella, cuento una curiosa y poco conocida propiedad del Caos en relación con el efecto mariposa. El efecto mariposa es una condición superflua del caos.


En el presente artículo, vamos a recuperar los conceptos necesarios del anteriormente citado y vamos a presentar la demostración de que, efectivamente, el efecto mariposa no es necesario para definir el caos. La demostración de este hecho no es difícil y tan sólo requiere conocimientos básicos de topología. Pero claro, estamos ya hablando de un nivel de estudios universitarios.


Vamos a recordar algunas cuestiones. Te recomiendo que antes de continuar, leas el artículo El Efecto Mariposa: vaya ¿timo?  y también le eches un vistazo a Caos lineal: ¿una paradoja?.

En primer lugar, el concepto de caos, aunque estaba en el acervo matemático, no tenía una definición clara hasta que Robert L. Devaney la introdujera en 1986. Según este matemático, un sistema dinámico, es decir, una aplicación continua de un espacio métrico en sí mismo, es caótica si cumple a la vez, las tres propiedades siguientes:

• Dependencia sensible respecto de las condiciones iniciales (efecto mariposa).
• Existe una órbita densa.
• Existe un conjunto denso de puntos con órbita periódica.

Veamos qué significa cada una de estas tres propiedades.

Antes de empezar, dado un punto , su órbita es el conjunto , donde .

es sensible respecto de las condiciones iniciales siempre que exista una constante de sensibilidad (que sólo depende de ) tal que para cada y cada existe y tales que y . Es decir, no importa cómo de cerca busquemos, que siempre encontraremos un punto de forma que más tarde o más temprano, su órbita se aleja de la de una cierta constante prefijada .


La segunda condición nos dice que existe un punto tal que para cada punto y cada , existe tal que .


Finalmente, la tercera condición nos dice que para cada punto y cada existe un punto periódico , tal que . Recordemos que un punto es periódico (o tiene una órbita periódica) cuando existe tal que .


Bien, pues ahora que sabemos todo lo que hay que saber, vamos a demostrar nuestro resultado.


Teorema: Sea un espacio métrico sin puntos aislados. Si posee un punto con órbita densa y un conjunto denso de puntos periódicos, entonces es sensible respecto de las condiciones iniciales.


Demostración: Antes de empezar, si es un espacio métrico sin puntos aislados, tenemos que si existe un punto con órbita densa, entonces existe un conjunto denso de puntos con órbita densa. En efecto, sabemos que es densa, pero para cada se tiene que y este conjunto sigue siendo denso, pues sólo hemos quitado una cantidad finita de puntos a un conjunto denso (para que esto sea cierto, es para lo que es necesario que no haya puntos aislados). Resumiendo, sabemos que hay un conjunto denso de puntos con órbitas densas.


En primer lugar, elijamos dos puntos periódicos diferentes y . Como sus respectivas órbitas y son periódicas, han de ser finitas. Sea , es decir, la distancia entre ambas órbitas. Ahora, fijado un punto , es claro que o bien o bien , en cualquier caso, hemos probado lo siguiente:

Existe 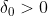tal que para cada 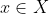existe un punto periódico 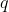de forma que .

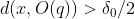Pues bien, vamos a demostrar que es sensible respecto de las condiciones iniciales y con constante de sensibilidad . A por ello.


Sea y (podemos suponer, sin pérdida de generalidad, que ). Como el conjunto de puntos periódicos es denso, existe un punto periódico tal que .


Tal y como hemos visto, dado existe un punto periódico tal que .


Ahora, sea el periodo de , y sea , donde es la bola de centro y radio , es decir, . Como es continua, se tiene que es una intersección finita de conjuntos abiertos (una aplicación es continua si la preimagen de un abierto es un abierto), por lo tanto, es un abierto. Además, es obvio que , pues para cada se tiene que . Por lo tanto, existe un número tal que .


Ahora, sabemos que existe un conjunto denso de puntos con órbita densa, por lo tanto, existe un punto con órbita densa tal que . Como es densa, existe un tal que , de donde deducimos que . Y esto significa que para cada se tiene que .

Ya estamos casi a punto. Sea la parte entera de . De esta forma, se tiene que y, por lo anterior, .


Ahora ya sólo nos queda darnos cuenta de que, como es el periodo de , se cumple que y aplicando la desigualdad triangular tenemos que:

.

Por un lado, sabemos que 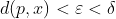; por otro 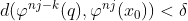; y finalmente, como 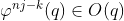y 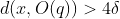, se tiene que 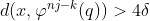. En resumen, tenemos que .


Y ya llegamos al final. Usando la desigualdad triangular, se tiene que o bien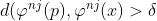 o bien Pero como 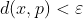y 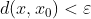, en cualquiera de los dos casos hemos demostrado la existencia de un punto 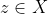y un natural 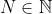(en realidad 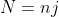)  tales que 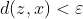y 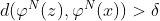. Por lo tanto, 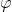es sensible respecto de las condiciones iniciales y con constante de sensibilidad .

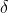Y aquí acaba la demostración.


Bueno, sé que no ha sido fácil para muchos de vosotros, pero de vez en cuando hay que ir metiendo un poco de nivel. Como ya eh dicho antes, esta demostración, en realidad, utiliza muy poca batería de conocimientos matemáticos: una distancia y el concepto de densidad. Creo que está al alcance de cualquier estudiante de primero de matemáticas e, incluso, de primer curso de ingenierías y física. Y si hay algo que no entiendes, pues ya sabes qué tienes que tratar de aprender.

Tito Eliatron Dixit


PD1: La referencia principal de esta demostración es la que aparece en J. Banks y otros, On Devaney’s definition of chaos, Amer. Math Month.99 4 (1992), 332-334. http://dx.doi.org/10.2307/2324899 Aunque la demostración no es exactamente la misma, sino que la he modificado lo suficiente como para no tener que introducir el concepto de transitividad topológica que es mucho menos intuitivo que el de existencia de órbita densa.


PD2: Esta entrada participa en la Edición 3.141 (Abril) del Carnaval de Matemáticas, cuyo anfitrión es el blog DesEquiLibros.