Desde que somos pequeños, la idea de "medir" ha estado siempre entre nuestras preferidas. ¿Quien no se ha medido (la altura) durante varios días y poniendo marcas en una pared? ¿quien no ha comparado sus notas con la de sus compañeros (hemos medido nuestros conociminetos)?
En Matemáticas, el concepto de
medida no es exactamente el mismo que tenemos asimilado, pero en realidad se le parece mucho. Una medida es una aplicación que a cada subconjunto de un conjunto dado le asigna un número positivo o nulo con las dos únicas siguientes condiciones:
- La medida del conjunto vacío (de la nada) es siempre 0.
- SI tenemos muchos (una cantidad numerable) elementos que no se cortan entre sí (que son disjuntos) la medida de todos ellos juntos es la suma de las medidas de cada uno de ellos individualmente.
Con esta pequeña definición, existen muchas cosas que son medida. En particular, la "longitud" en la recta real
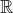
, el área en el plano
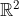
, el volumen en el espacio tridimensional
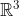
,... son todas medidas. Pero para que de verdad posean las dos propiedades anteriores, hace falta restringir un poco los conjuntos que podemos medir.Los conjuntos que se pueden medir se denominan
Conjuntos Medibles y prácticamente cualquiera que te puedas imaginar lo es (intervalos, polígonos, poliedros....). De hecho, si tenemos un conjunto medible y lo
movemo, el resultado sigue siendo un conjunto medible y además, la medida de ambos coincide (el área de un círculo no depende de dónde lo pintemos, sino sólo de su radio; y lo mismo para la longitud de un segmento, o el volumen de una pirámide,...).
Sin embargo vamos a construir a continuación un conjunto que no va a ser posible medirlo. El ejemplo se debe al matemático italiano
Giuseppe Vitali.
Vamos a partir del intervalo unidad
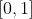
. Sobre él, diremos que dos números
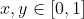
están relacionados si
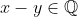
. Esta relación es una
relación de equivalencia, lo que supone que el conjunto
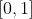
queda dividido en lo que se conoce como
Clases de Equivalencia, es decir, metemos un un mismo saco a todos los números que están relacionados entre sí. El problema es que, en realidad, hay infinitas de estas clases.
El conjunto de Vitali es
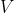
un conjunto formado por un único representante de cada una de las clases de equivalencias en que queda dividido
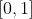
. ¿Problemas? no. Ah! bueno sí, que para poder hacer esto hay que usar el
Axioma de Elección, lo que a veces no está bien visto (por cierto, si no sabes de qué va este axioma, quizás este
símil con calcetines te ayude).
Bueno, dejemos a un lado lo del axioma y veamos que el conjunto así construido no puede medirse (que no se le puede asignar una longitud, vamos).
En primer lugar, como los recionales son numerables, entonces
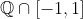
también lo será, así que vamos a enumerarlos y los llamamos
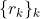
. Ahora, para cada uno de estos racionales, llamamos
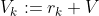
, es decir, nos quedamos con los
trasladados del conjunto de Vitali. Estos conjuntos resulta que son disjuntos dos a dos. En efecto, si
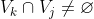
, existirían
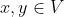
tales que
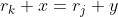
, de donde
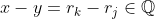
y tendríamos que
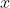
e
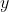
estarían relacionados, es decir, están en la misma clase de equivalencia. Pero como
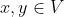
y en él sólo puede haber un representante de cada clase de equivalencia, debe ser
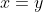
, por lo que
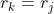
y
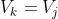
.
Una vez que sabemos que los
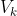
son disjuntos dos a dos, nos vamos a quedar con la unión de todos ellos, es decir,
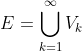
.
A ver, Tito, que ya estamos haceiendo cosas demasiado raras. Venga, va, para que no nos perdamos, os diré que
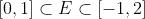
. En efecto, si
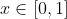
, tomamos
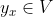
tal que
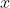
esté relacionado con
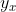
, es decir, tomamos el elemento de
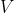
que está en la misma clase de equivalencia que
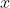
. Entonces
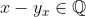
, y, además,
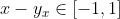
(pues
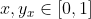
). Por lo tanto, existe
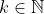
tal que
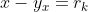
, de donde
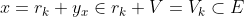
. Por otro lado, para cada $k\in\Bbb N$, se tiene que
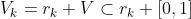
, pero como
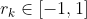
, se tiene que
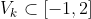
.
Vale, ya sabemos que este conjunto
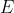
está entre los intervalos
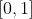
y
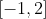
, luego su longitud debe estar entre 1 y 3, es decir,
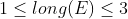
. Pero hemos visto que
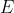
está formado por una cantidad numerable de conjuntos disjuntos, luego la longitud de
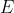
debe ser la suma de las longitudes de los conjuntos. Así, tenemos que $long(E)=\sum_{k=1}^\infty long(V_k)$.
Y ahora viene lo bueno. Resulta que los
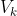
eran trasladados de un mismo conjunto
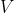
, por lo tanto, SUPONGAMOS QUE
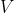
ES MEDIBLE, es decir, supongamos que a
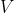
le podemos asignar una longitud: pongamos
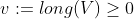
. Entonces, todos los
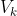
deben ser medibles y, además, tener la misma longitud que
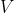
. Así que al final tenemos que
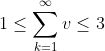
.
Uy uy uy, que la cosa se pone fea. Si
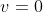
, entonces tendríamos que
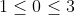
IMPOSIBLE, pero es que si
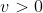
, entonces resulta que

y es peor aún.
Solución: no podemos asignar a
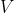
una medida, es decir,
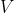 no es medible
no es medible.
En fin, que si aceptamos el uso del Axioma de Elección, acabamos de construir un conjunto verdaderamente RARO RARO RARO.
Tito Eliatron Dixit
PD: Esta entrada participa en la la
Edición 2.6 del
Carnaval de Matemáticas cuyo anfitrión es el blog
La Vaca Esférica.
PD2: La mayor parte de esta entrada está basada en la construcción del conjunto de Vitali que se hace en el libro
Integración de funciones de varias variables de
José A. Facenda Aguirre y
Francisco J. Freniche Ibáñez.

¡Muchísimas gracias! Entendí tu demostración. :)
ResponderEliminar