El efecto mariposa
A finales del siglo XIX, los matemáticos se esforzaban por comprender la naturaleza del caos. Un fenómeno que a menudo se asocia a este concepto es el conocido como Efecto Mariposa
El simple aleteo de las alas de una mariposa en Brasil puede provocar un tornado en Texas.
 |
| Imagen obra de Francisco Manuel |
Otra característica del caos es la existencia de condiciones iniciales que conducen a cualquier configuración posible del sistema: Una nave espacial que parta de un lugar privilegiado acabará visitando cada rincón del espacio. En la jerga matemática, su trayectoria recibiría el nombre de órbita densa.
El caos en matemáticas
En 1986, el matemático norteamericano R. Devaney [1] propuso una definición de caos que, a primera vista, impone condiciones muy fuertes. Según él, un sistema dinámico es caótico si se verifican, a la vez, las tres propiedades siguientes:
- Dependencia sensible respecto de las condiciones iniciales.
- Existe una órbita densa.
- Cerca de cada punto, siempre pasa una órbita periódica.
Sistemas Dinámicos
Un Sistema Dinámico (discreto) viene dado por una función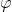 de un conjunto
de un conjunto 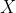 en sí mismo, es decir,
en sí mismo, es decir, 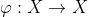 .
.
Si llamamos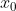 al estado inicial, los siguientes estados se calculan utilizando la fórmula
al estado inicial, los siguientes estados se calculan utilizando la fórmula  , con
, con  , donde
, donde 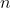 se interpreta como el tiempo. La órbita de un punto
se interpreta como el tiempo. La órbita de un punto 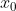 viene dada por la sucesión
viene dada por la sucesión  .
.
Un Sistema Dinámico (discreto) viene dado por una función
Si llamamos
 |
| Dependencia sensible respecto de las condiciones iniciales: una mesa de billar con obstáculo. Dos bolas lanzadas con ángulos similares, pero con comportamientos muy diferentes. |
 |  |
| Una órbita periódica: el cometa Halley Este cometa gira alrededor del sol en una órbita elíptica. Su periodo es de 75 años. | Una órbita densa dentro de un anillo |
Un ejemplo sencillo.
¿Son demasiado fuertes las condiciones impuestas por Devaney? Al contrario. Estas condiciones las verifica un sistema dinámico muy simple: el descrito por la función
Es fácil encontrar otras órbitas periódicas. De hecho, cerca de cada punto se puede encontrar otro punto con órbita periódica. La tercera condición de caos según Devaney es, por tanto, verificada por este sistema.
Con respecto a la dependencia sensible de las condiciones iniciales, vamos a ilustrarlo con un ejemplo, que se muestra en la tabla de más abajo. Para el estado inicial
Órbita original
|
Órbita perturbada
| |
0.16
|
0.17
| |
0.32
|
0.34
| |
0.64
|
0.68
| |
0.72
|
0.64
| |
0.56
|
0.72
| |
0.88
|
0.56
| |
0.24
|
0.88
|
Si bien esto es más difícil de ver, también se puede demostrar que este sistema tiene órbitas densas. El sistema dinámico dado por la función
Sistemas no lineales
El sistema definido por la función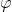 es no lineal. En efecto, si fuera lineal, se tendría que para cada par de puntos
es no lineal. En efecto, si fuera lineal, se tendría que para cada par de puntos 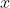 e
e 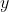 , sería
, sería  .
.
Sin embargo, si e
e  , sería
, sería  ., mientras que
., mientras que  y, por lo tanto,
y, por lo tanto,  .
.
El sistema definido por la función
Sin embargo, si
Existencia de caos lineal
En 1991, G. Godefroy y J.H. Shapiro [2] proponen aceptar la definición de caos en el sentido de Devaney, también para sistemas lineales. Tenían en mente un resultado clásico de G.R. MacLane de 1952 [3].
Este último afirmó que el operador de derivación
El caos lineal, por tanto, existe.
Y sorprendentemente, y como prueba el operador de derivación, no es ni siquiera necesario construir operadores de una gran complejidad para observar este fenómeno.
Un sistema lineal.
El sistema dinámico definido por el operador derivación es lineal.
Si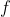 y
y  son dos funciones derivables y
son dos funciones derivables y 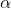 es un número real cualquiera, se tiene que
es un número real cualquiera, se tiene que  y
y  .
.
El sistema dinámico definido por el operador derivación es lineal.
Si
¿De dónde proviene el desconocimiento del caos lineal?
Imponer la linealidad a un sistema, constituye, a pesar de todo, una restricción importante: el caos lineal sólo puede ser observado en sistemas en espacios de dimensión infinita, como por ejemplo, el espacio de todas las funciones indefinidamente derivables. Es probable que la imposibilidad del caos lineal en dimensión finita sea la base de este desconocimiento. Sin embargo, una vez que esta barrera se cruza, todo es posible. Un resultado de N. Feldman de 2001 [4] muestra que un sistema lineal de dimensión infinita puede adoptar cualquier comportamiento irregular observado en un sistema no lineal.
Un espacio de dimensión infinita.
El espacio de las funciones infinitamente derivables es de dimensión infinita, ya que tiene un número infinito de funciones básicas con las que se pueden representar a todas las demás funciones de este espacio.
Por ejemplo, los monomios , con
, con  forman un conjunto infinito e independiente: ningún monomio se puede expresar como una combinación lineal de otros monomios. Sin embargo, para llegar a una base, ¡todavía es necesario añadir otras funciones!
forman un conjunto infinito e independiente: ningún monomio se puede expresar como una combinación lineal de otros monomios. Sin embargo, para llegar a una base, ¡todavía es necesario añadir otras funciones!
El espacio de las funciones infinitamente derivables es de dimensión infinita, ya que tiene un número infinito de funciones básicas con las que se pueden representar a todas las demás funciones de este espacio.
Por ejemplo, los monomios
Una teoría en plena expansión…
El trabajo de Godefroy y Shapiro ha sido un verdadero desencadenante en la investigación sobre caos lineal. Hoy en día, numerosos equipos de todo el mundo estudian este fenómeno. En 2004, dos jóvenes matemáticos franceses, S. Grivaux y F. Bayart [5], observaron un comportamiento sin precedentes: existen órbitas, llamadas frecuentemente recurrentes, que son densas y, sin embargo, muestran un fuerte aspecto de periodicidad. Más concretamente, si nos fijamos en un punto cualquiera del espacio, existe un tiempo
Intentemos imaginar por un momento el comportamiento de una nave dentro de nuestro universo que siga una trayectoria con esta propiedad. Si por ejemplo, para el Sol tenemos que
… y de cuestiones todavía abiertas
Si bien un comportamiento como éste no había sido observado previamente para un sistema no lineal, Grivaux y Bayart demostraron que el operador de derivación posee una órbita frecuentemente recurrente. Por tanto, parece natural preguntarse si cualquier sistema caótico posee una tal órbita. Nadie sabe aún la respuesta a esta pregunta. El caos lineal todavía no nos ha contado todos sus secretos
Tito Eliatron Dixit
Bibliografía (por orden de aparición):
[1] L.R.Devaney, An introduction to chaotic dynamical systems, Benjamin/Cumings, Menlo Park, CA, 1986.
[2] G.Godefroy y J.H.Shapiro, Operators with dense, invariant, cyclic vector manifolds, J. Funct. Anal. 98 (1991), 229-269.
[3] G.R.MacLane, Sequences of derivatives and normal families, J. Analyse Math. 2 (1952/53), 72-87.
[4] N.Feldman, Linear Chaos? (2001) PDF disponible en
http://home.wlu.edu/~feldmann/pdffiles/LinearChaos.pdf
[5] F.Bayart y S.Grivaux, Hypercyclicité: le rôle du spectre ponctuel unimodulaire, C. R. Math. Acad. Sci. Paris 338 (2004), 703-708.
Nota de Tito Eliatron: El presente artículo es una traducción de un original de K.G.Grosse-Erdmann y su alumno Quentin Menet publicado en Interstices el 24 de febrero. El primer autor ha dado permiso a este blog para su traducción. Las imágenes que no tenían copyright, han sido extraídas del propio artículo original.
PD: Esta entrada participa en la Edición 3.14 del Carnaval de Matemáticas cuyo anfitrión en esta ocasión es el blog Hablando de Ciencia.


Es realmente impresionante cómo puede alterar la comprensión del infinito nuestra visión del mundo.
ResponderEliminarHola:
ResponderEliminar¿ qué se entiende por dimensión de un espacio ? Sólo conozco el concepto para espacios vectoriales, pero no para sistemas de funciones.
Entiendo que tiene que ver con la cardinalidad de una base de elementos generadores , pero desconozco la definición exacta =
Por ejemplo, ¿ cual es la dimensión de f(x) = 1 - | 2x -1 | con 0 <= x <= 1 ?
Gracias