Lo importante... no participar (o aprende estadística con El Hormiguero)

Hace unos días estaba yo viendo (jajaja, "yo viendo" "lloviendo" jajaja -ejem, perdón por el momento Peter Griffin-) El Hormiguero. Casi al final del programa, decidieron hacer un juego con el público, con el fin de regalar (o no) un juego de mesa del programa a cada uno de los asistentes. El juego consistía en lo siguiente: cada uno de los asistentes como público debía quitarse un zapato y, desde su asiento, lanzarlo (cual periodista irakí a Bush) al interior de una cuba que estaba más o menos en el centro del plató. Si al final del proceso quedaban menos de 30 zapatos fuera de la cuba, todos los asistentes se llevaban a su casa el susodicho juego de mesa; caso contrario... pues no se lo llevaban. El resultado fue favorable al público y todos se fueron contentos a casa.

Esto puede parecer un juego más de los que se hacen en la tele, pero a mi me llamó la atención un detalle. El caso es que no era la primera vez que veía este juego en El Hormiguero. Unas semanas antes también hicieron el juego, pero en esa ocasión, recuerdo que para ganar, impusieron la condición de que quedaran menos de 25 zapatos fuera. El resultado ya no fue tan satisfactorio para el público.

Con estos datos encima de la mesa, uno, que ya tiene las orejas tiesas con cuestiones así, percibe que el hecho de variar el número de zapatos fuera debería ser muy importante. Así que me puse a hacer algunos números... y aquí tenéis los resultados.



Como decía un profesor mío... vamos a estudiar el caso general y ya luego particularizamos.

Lo primero que hay que tener en cuenta es que, cada miembro del público lanza de forma independiente su zapato, es decir, que el lanzamiento de uno, no interfiere en el de otro. En realidad, esto no es cierto del todo, pero es que si no tenemos en cuenta este detalle, los cálculos se hacen imposibles. Así que podemos suponer que cada lanzamiento individual es un experimento independiente del otro.

Vamos a suponer que hay personas en el público, que cada uno de ellos tiene una probabilidad de encestar su zapato en el cajón (por lo tanto, hay una probabilidad de fallar) y que para que el grupo gane, hace falta que haya menos de zapatos fuera.

Vamos al lío. ¿Cual es la probabilidad de que gane el grupo? Vamos a responder de dos formas.

Llamamos al número de zapatos que quedan fuera del cajón. Para que gane el grupo, hace falta que haya 30 o menos zapatos fuera, por lo que habrá que calcular, la probabilidad de que haya exactamente zapatos fuera desde hasta , es decir:

Si tienes conocimientos de distribuciones estadísticas discretas, verás que se trata de una distribución de Binomial con experimentos (cada uno de los lanzamientos) y probabilidad de éxito (la probabilidad de fallar el lanzamiento, es más conveniente así), es decir, . Por lo tanto, se tiene que

 

y

.

Vale, si no tienes conocimientos estadísticos, o bien no los recuerdas bien, vamos a a reobtener la fórmula de de una forma razonada.
Para que entre los miembros del público haya zapatos fuera hace falta que también haya zapatos dentro. Como la probabilidad de no encestar es y la de encestar es , se tiene que la probabilidad de que haya exactamente zapatos fuera es . Pero esto no coincide con nuestra fórmula... aún. Lo que hemos hallado corresponde a una configuración específica del público. Me explico. Imaginad que en cada asiento hay un número del 1 al . Esta es la probabilidad de que los que ocupan los asientos del 1 al fallen y los del al encesten. Pero a nosotros nos da igual que los que fallen sean los primeros que los últimos que los de en medio, que salteados. Así que si calculamos todas las formas de colocar a los que no encestan en los asientos numerados, sólo habrá que multiplicar ambos números (la probabilidad calculada y el número de configuraciones). Por tanto, habrá que calcular el número de formas en las que podemos elegir números de entre sin que me importe el orden en el que salgan pero sin que tampoco se repitan; ese número es, precisamente el coeficiente y lo podemos interpretar así.
Hay formas de ordenar a personas (piensa: para el asiento 1, hay candidatos; para el 2, ; para el 3; ; ... ; para el asiento ya sólo quedan 2 candidatos y para el último asiento, un único candidato). Pero de esas personas, seleccionamos que fallan y que se pueden ordenar de cualquier manera; y lo mismo con las que aciertan. Por tanto el número de formas de sentar a las personas una vez prefijadas las que aciertan y las que fallan es, justamente .



Vale, pues resumiendo todo, si tenemos personas con probabilidad de encestar y queremos que el grupo gane si el número de personas que encestan es inferior a , la probabilidad de que esto ocurra es:

.

Perfecto, ya tenemos el caso general. Ahora vamos a particularizar nuestro estudio a los dos casos. En primer lugar, hay que establecer los datos del problema. El número lo dan en ambos días ( uno y el otro). Sin embargo, los otros dos datos (el número de personas y la probabilidad de acertar ) los desconocemos.
Si uno ve el programa de El Hormiguero y mira una panorámica del público, observa que éste se distribuye en una grada con 4 filas en las que pueden caber, aproximadamente unas 20 personas, más una pequeña grada lateral con una fila superior de unas 10-15 personas arriba y otras tantas abajo. En total eso da una cifra aproximada de 100 personas en el público o, a lo más, 110. ¿Es ese el dato ? No. El dato corresponde con el número de personas que participan en el juego y viendo el programa se observa que hay unos cuantos que no quieren desprenderse de un zapato (bien por vergüenza, por desgana... o porque son muy listos). Así que parece lógico suponer un número algo menor de esos 110, por ejemplo, (y creo que estoy siendo muy generoso).
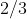
Finalmente, dada la situación respecto del público y el tamaño del cajón en el que encestar los zapatos, creo que es más fácil encestar que fallar y diría que 2 de cada 3 personas aciertan su lanzamiento, por lo tanto, podríamos asignar a un valor de (y creo que estoy volviendo a ser generoso).


En el primer caso, en que , la probabilidad de ganar el premio es poco más o menos del 4,5%; mientras que en el caso en que resulta ser casi del 28%.
Anda! qué curioso. Un cambio, a priori tan insignificante, me da como resultado una variación tremenda de la probabilidad final.
Pero vamos a tomar unos datos, a mi modo de ver, más realistas. Supongamos que (ya dije que creía que habría unas 100 personas, de las que algunas no participan en el juego) y que (vamos a aumentar ligeramente la probabilidad de acertar). Ahora para [m=25], la probabilidad pasa a ser del 37%; pero resulta que para ahora la probabilidad es del 79%.
¿Qué puedo concluir de estos datos? Pues que la dirección del programa tiene claro

Aquí os dejo con una tabla de probabilidades, asumiendo que para diferentes valores de desde 30 hasta 120 (aumentando de 5 en 5) para 3 posibles valores de , los 2 estudiados y uno algo menor todavía (, con el que las diferencias aún son más marcadas).

Público	m=20	m=25	m=30
30	0.999993	1	1
35	0.999777	1	1
40	0.997581	0.999995	1
45	0.986477	0.9999	1
50	0.952236	0.999067	0.999997
55	0.879215	0.994812	0.999957
60	0.762217	0.980426	0.999636
65	0.612995	0.945199	0.997984
70	0.45502	0.878681	0.99202
75	0.311784	0.777251	0.975846
80	0.197847	0.647937	0.941252
85	0.116822	0.506334	0.880652
90	0.0645294	0.370293	0.791141
95	0.0335234	0.253646	0.677034
100	0.0164629	0.16313	0.549124
105	0.00767839	0.0988259	0.421082
110	0.00341587	0.0565981	0.305153
115	0.00145505	0.0307552	0.209197
120	0.000595534	0.0159137	0.135923

Como podréis ver, y de ahí el título del post, a medida que el número de jugadores disminuye, aumenta considerablemente la probabilidad de que el grupo gane (obviamente si el suceso "Gana el grupo" es seguro, pues siempre quedarán "menos de " zapatos, al haber exactamente jugadores). Para se pude observar que desde el caso 120 jugadores hasta el caso 100 jugadores (una diferencia de 20), la probabilidad de ganar aumenta un 40%. En el caso entre 105 y 85 jugadores, el salto es del 49%; mientras que en el caso , el salto de 85 a 65 jugadores es del 50%.

Y esto ocurre porque los términos suma que nos da la probabilidad de ganar, al igual que pasa con los números del Triángulo de Pascal, son más grandes en el centro que en los extremos; y si nos fijamos, en las condiciones del problema, (90 personas en el público y pasar de 25 a 30), estamos quitando 5 de los términos centrales de la suma (fijaos que si la suma se hace trivialmente 1).

¿Y todo esto para qué? Pues para divertirme, nada más. Eso sí. ¿Y si se utilizase esto para enseñar la distribución Binomial a unos alumnos? ¿Sería posible que les gustara más que de la forma tradicional con los aburridos lanzamientos de monedas? Yo os lo dejo ahí, por si algún profesor le apetece usar esta idea.


Tito Eliatron Dixit


PD1: Os dejo los enlaces a los programas de los que hablo: Programa en el que imponen 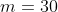y programa en el que imponen .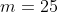

PD2: En el los casos en los que trabajamos ( ó ) estamos en condiciones de aproximar la Binomial de parámetros y por una Normal de parámetros y . Así, bastaría con pasar a tipificar nuestra normal y calcular a través de la tabla correspondiente de la normal.

PD3: Con esta entrada participo en la Edición 3.141592653 del Carnaval de Matemáticas cuyo anfitrión es el blog Que no te aburran las M@TES.